前一篇最后追加了用SageMath解微分方程的示例,官方文档里面也提到了符号运算默认调用的还是Maxima软件包。本来想追加一段直接使用「原版」Maxima的示例,但是SourceForge.net的下载被防火长城阻挠了。注:已追加。
然后按照恶补计划,开始看「几何」了,本来应该是去年的任务,在流水账开头也提到了重点就是几何,这部分是当年上学的时候由于应用数学系安排辅修计算机而被砍掉的课程,属于真・没学过。
但是由于政治和意识形态斗争需要,支线任务消耗的时间和精力过多,并且色目宣传工作者兼玄学家的薪水似乎极大充沛导致工作热情超高,不打自招的爆料当中重要情报如车载斗量不可胜数,于是处理情报也消耗了相当多时间精力。总之没来及。
今年以来,通过一系列深入揭批政治和意识形态内容和政治和意识形态斗争新动向的本职工作,相关「学术」铺垫已经完成,现在可以打开天窗说亮话了也。
在《知乎问答〔№328〕有哪些具有方言特色的笑话?》当中提到了兲朝特色几何方向的名言「心里没点陈数?」
自称代表了「学术圈」(或曰「高学历精英社交圈」)的知乎,已经有大拿进行过肤浅的文本分析,说此「方言」乃「胶辽官话」,是《马关条约》割让的山东半岛和辽东半岛地盘上流行的问候用语。
也就是说,乍一看市面上充沛的「东北人」素材,很可能只是大连附近一小片地方从事面向特大日本帝国外交工作的公务员当中部分负责「路径依赖」事宜的岗位职责;而口口声声「反汉贱种中国通」的山东公务员,也很可能只是局限于青岛烟台等地,早已被「满铁调查课」渗透得如同筛子一样,自己开会拿着文件副本,正本跑到大连那里去了也。
范某截图备份于此
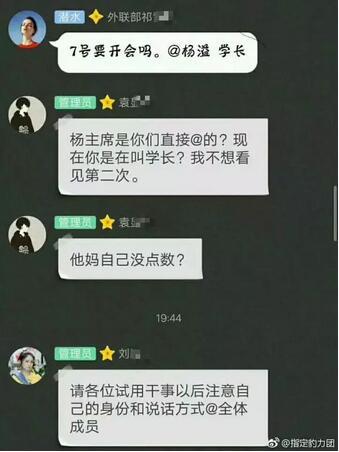
前一篇当中使用「京师大学堂」教材白纸黑字举例证明其内部政治和意识形态斗争的激烈程度。还有个「清政府,北大荒」的例外,说京师大学堂「学生会」主席也是官运亨通,只不过按照顺序上台一个拿下一个来去匆匆,目前正好轮到现任中堂大野家龙裔,后面替补还没浮出水面。
铺垫结束,言归正传。
按照京师大学堂公开传播的数学系课程,顺序是「(古典)微分几何」→「微分流形」→「黎曼几何」,正好三门课程都有陈维桓出品的教材,想必「陈数」充沛。
同样,陈维桓《微分几何》前言当中,也提到了Mathmatica,并赞美一名童年才俊使用Matlab之后「表露出来的兴奋心情至今令人难忘」,还专门写了一篇附录讲述使用Mathematica炮制课件的简介。
所以,支线任务又出现了,那就是用SageMath和GNU Octave把这附录当中提到的内容进行实践。优先级未必多高,参数方程定义好之后都是大同小异,示例会慢慢补充。其它课程也一样,手头国人「编著」的Matlab的通俗读物有那么十几本吧,可供GNU Octave实践时借鉴。
如果恶补中用得比较频繁,可能会单独开个栏目存放这些代码和截图,需要引用的时候给出链接就够了。
正因为当年真・没学过,所以现在按照「寻找脑洞」的原则把《微分几何》翻了一遍,不能说「学」,里面公式都未必能记住,不过可以在使用Maxima/GNU Octave实践课件的过程中略作复习。顺便发现,GNU Octave最新版5.1已经发布。
但是呢,这个课程本身的程度,就是为了在「老三篇」之后直接加以运用的,算是基础课之一,里面很多都是后来于其它场合道听途说过的「常识」。因此脑洞也没找到多少,直到看到附录(不属于课程内容)里面有一句「自共轭线性变换如果有r重特征值,则对应的特征向量是r维子空间」,忽然想起之前的脑洞了。
前面(链接)提到了,看到《概率论》时揣测「分布函数三种基本类型是啥空间的一组基」,于是惦记着找个无穷维空间上自共轭算子存在三重特征值,并且特征向量刚好是三种分布函数基本类型。
再结合更早的设定,若是能找到有(至少)俩三重特征值的,一套对应「卡壳世界」三维空间本身,另一套对应其「随机性」。当然目前只是脑洞而已,若有思路,再不惮以最大的恶意揣测这俩「小三」之间存在着什么见不得光的神秘联系。
到这里又得老生常谈「不忘初心牢记使命」了,我说构思「数学幻想作品」的基础是构造一个「与本位面几乎处处一致」的架空世界,仍然无一字无来历。
可以参考最近两会期间充沛在知乎首页推荐当中的唯物主义童年才俊的猖狂进攻,还是「民科」「杠精」「反社会人格」之类司空见惯的字眼。
其中包括但不限于对霍伊尔「稳恒态宇宙」假设的嘲讽,啥在唯物主义实验物理学家指着一堆唯物主义设备的输出数据当中的皮亚诺或拉格朗日「余项」叫嚣着发现了支持「创世纪」假说的唯物主义证据「微波背景辐射」之后就被扫入历史唯物主义の垃圾堆,而唯物主义理论物理学家纷纷面向耶路撒冷纳头便拜言必称哈利路亚。
这里还有个学术史上的典故,说当年为了普天同庆瑞典和挪威国王奥斯卡二世在1889年的六十大寿,悬赏征求太阳系的稳定性问题的解答,也就是力学当中的「多体问题」。事实都知道了,就连「三体问题」都只能有各种限制性特解。
那么我们生活的这个宇宙,还是特么稳定的么?为啥充沛在时间和空间当中各种「微扰」并不能带来「世界末日」然后一票耶路撒冷路径依赖工作者就得意忘形肆无忌惮的炒作弥赛亚眼瞅着就降临了顺之者昌逆之者亡呢?
所以,各种动力系统稳定性研究都已经深入到一定程度之上的现在,哪怕在理论上「微波背景辐射」也不过是个添头,好比大年三十晚上的兔子,有它过年,没它也过年。
一个没有「微波背景辐射」的架空世界,就是和本位面「几乎处处一致」,啥「创世纪の唯物主义证据」的影响是精确的零,无论惦记着中饱私囊的物理神童龙裔及其奴才如何在包括但不限于知乎等宣传阵地当中声嘶力竭的炒作宏大叙事望远镜和史无前例对撞机,都特么没区别。
补充:使用wxMaxima绘制参数方程形式的平面曲线
在陈维桓《微分几何》(第二版)的附录〈3.2.1〉中给出的Mathematica代码是这样的:
范某截图备份于此

而我在wxMaxima当中的实践是这样的:
范某截图备份于此
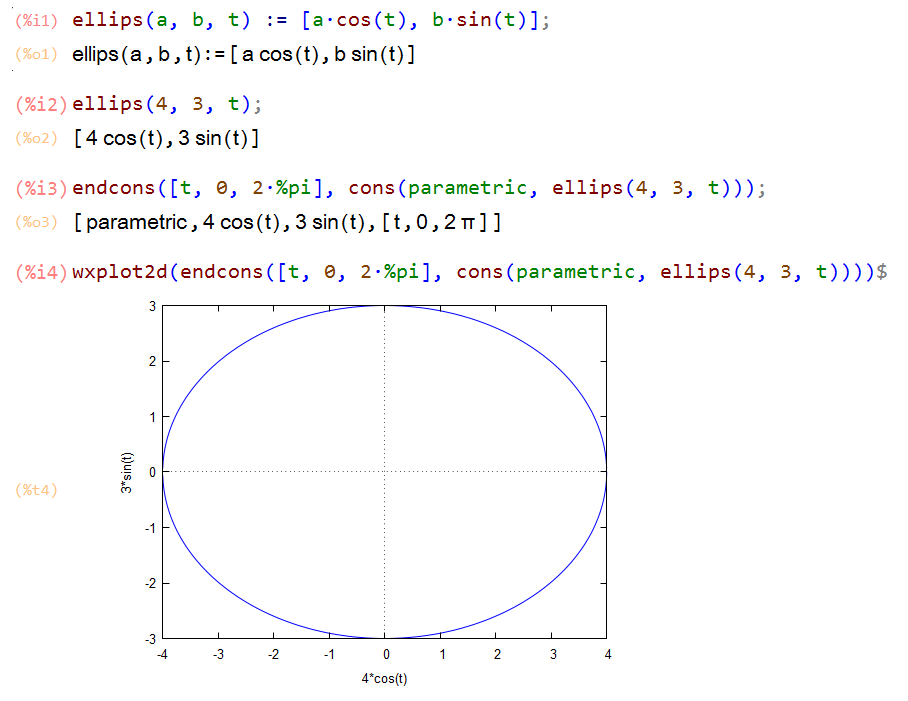
其中对应Mathematica「//Evaluate」代码的部分,就是Maxima「%i3」展开为「%o3」的形式。看上去很笨,我自己也不满意,但是一时找不到更优雅的方式。
究其原因,在于参数(Parameter
)方程的定义是个「列表」,需要以参数(Argument
)形式传递给绘图函数。从图中过程也可以看出,对应x(t)和y(t)的两项参数(Parameter
)表达式是直接作为调用参数(Argument
)的一部分,需要去掉「方括号」(对应Mathematica的「大括号」)。
按理说LISP最擅长处理的就是「LIST」吖,但是试了好几种方法都不能简单的展开。只能说,相关绘图函数的接口设计,是面向程序员而不是数学工作者的,使用「parametric」参数(Argument
)调用「plot2d」就直接放两项,而「plot3d」就是三项,没有对于「参数(Parameter
)方程(组)」作出进一步的抽象。
也就是说,实际上Maxima使用的是「借鉴了LISP形式的Maxima语言」,而Mathematica用的是自定义的「Wolfram语言」,结合使用场景才能评论便利与否。
这里仅举一例,其它相关内容,以及使用SageMath/GNU Octave的实践过程,会单独写一篇《三自课件运动》放在《囧斋随笔・与时俱进》之下。还是优先级不高并且内容不完整,除了提高自身素质之外的必要劳动之外,不会把时间精力消耗在技术细节之上,仍然按照「形而上者谓之道」原则进行坚决的政治和意识形态斗争,干好「本职工作」。
总之,不惮以最大的恶意揣测以京师大学堂为首的一票数学专业院系,在无法配合信息技术神童龙裔炒作「听都没听说过的新鲜名词」或配合物理神童龙裔炒作「宏大叙事史无前例唯物主义玄学观念」以诈骗官方预算并在民间非法集资的情况下,靠山吃山靠水吃水,羊毛出在羊身上。
百善の新时代当中的各级教育部门官僚,不是以与时俱进借口向学生们摊派消耗外汇进口的境外商业软件,就是以规定课件格式的方式逼迫教师们自带干粮自掏腰包配置工作环境。这种做法,与万恶的旧社会教育部门官僚指定关系户编纂的教材参考书并指定关系户开设的书店购买一模一样。